For the US curriculum, irrational numbers are introduced in year 8 (8.NS.A.1). In most textbooks, however, students are simply taught to distinguish between rational and irrational numbers, and then to estimate the square roots of 2, 5, or 7. If this is all that students are exposed to, they miss all the beauty and wonder (and mystery) of irrational numbers.
I find that the mystery and paradox involved is the very thing students enjoy the most about the topic. Sometimes, I might draw a number line on the board and talk about a number in between 2 and 3 such as 2.5. Then, we'll half that and find 2.25, then 1.125, etc. Students realize fairly soon that as we zoom in on the number line we could continue halving forever. This is an apt time to introduce Xeno's paradox. Last year, however, I tried a new approach to this exploration into infinity.
I created a spreadsheet and showed students that √7 is between √4 and √9, which means √7 is between 2 and 3. Students will usually guess 2.6 since √7 is closer to √9 than √4. Once I type 2.6 the spreadsheet automatically calculates the square value of 6.76. This lets us know that our guess of 2.6 is a little small.
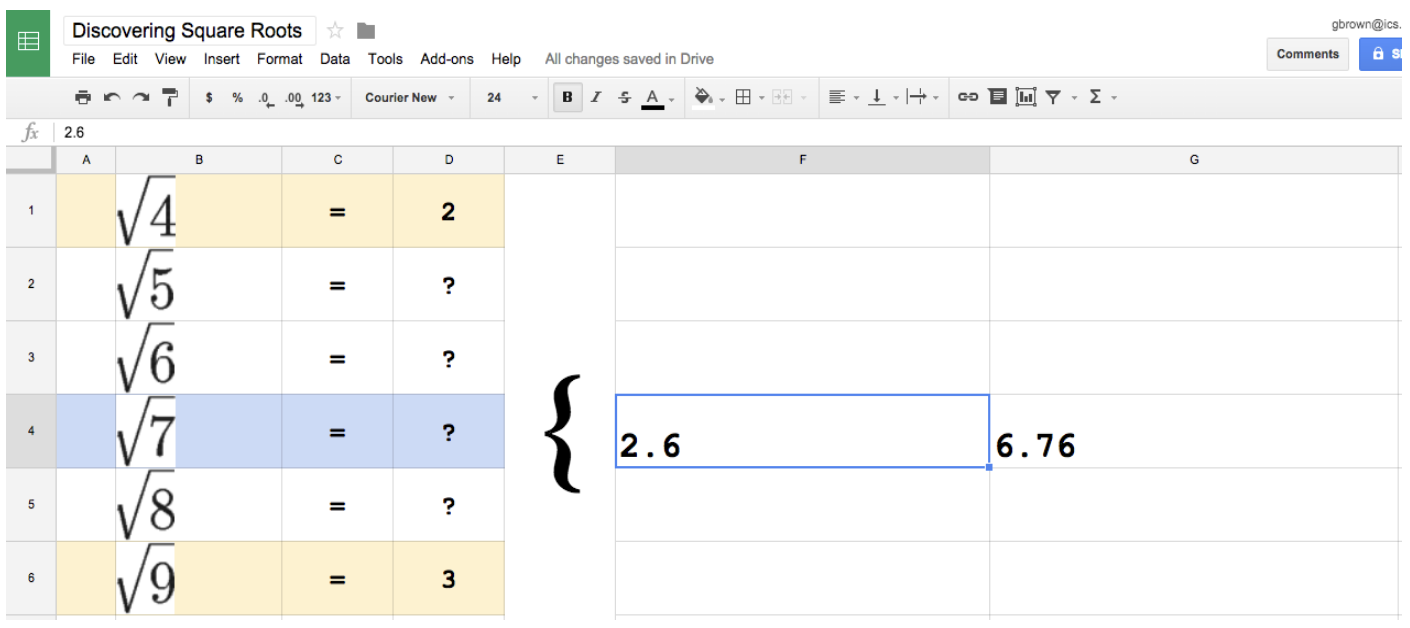
Next, students might guess 2.7 to see if 2.7*2.7 is exactly 7. We find out that 2.7 is too large since 2.7 squared is 7.29. At this point, I'll typically ask students what we should do. Quickly, someone will suggest 2.65.
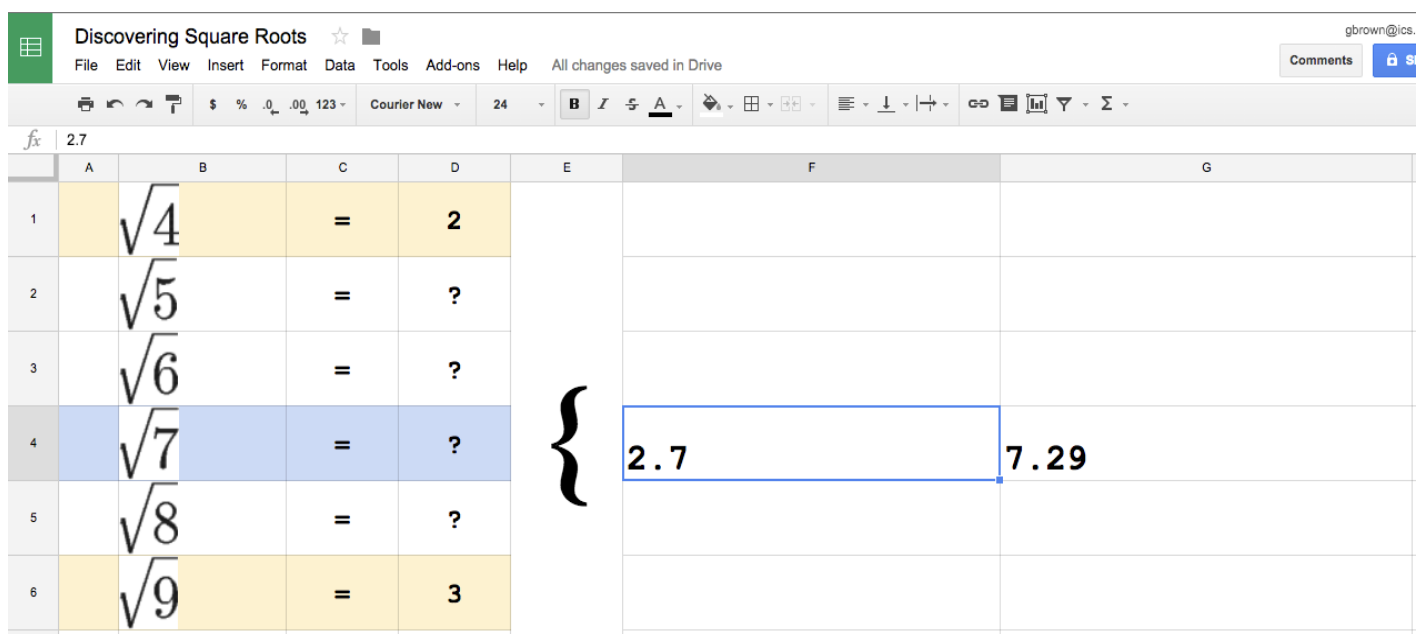
If I enter 2.65 into the spreadsheet, we see the result that 2.65^2 = 7.0225. This means that 2.65 is too large. Students now will suggest 2.64 or 2.63. I'll try these until we find that 2.65^2 = 2.9696 so the answer is somewhere between 2.64 and 2.65. At this point, students began getting competitive about guesses... some suggest 2.642, others 2.644, and others suggest 2.647.
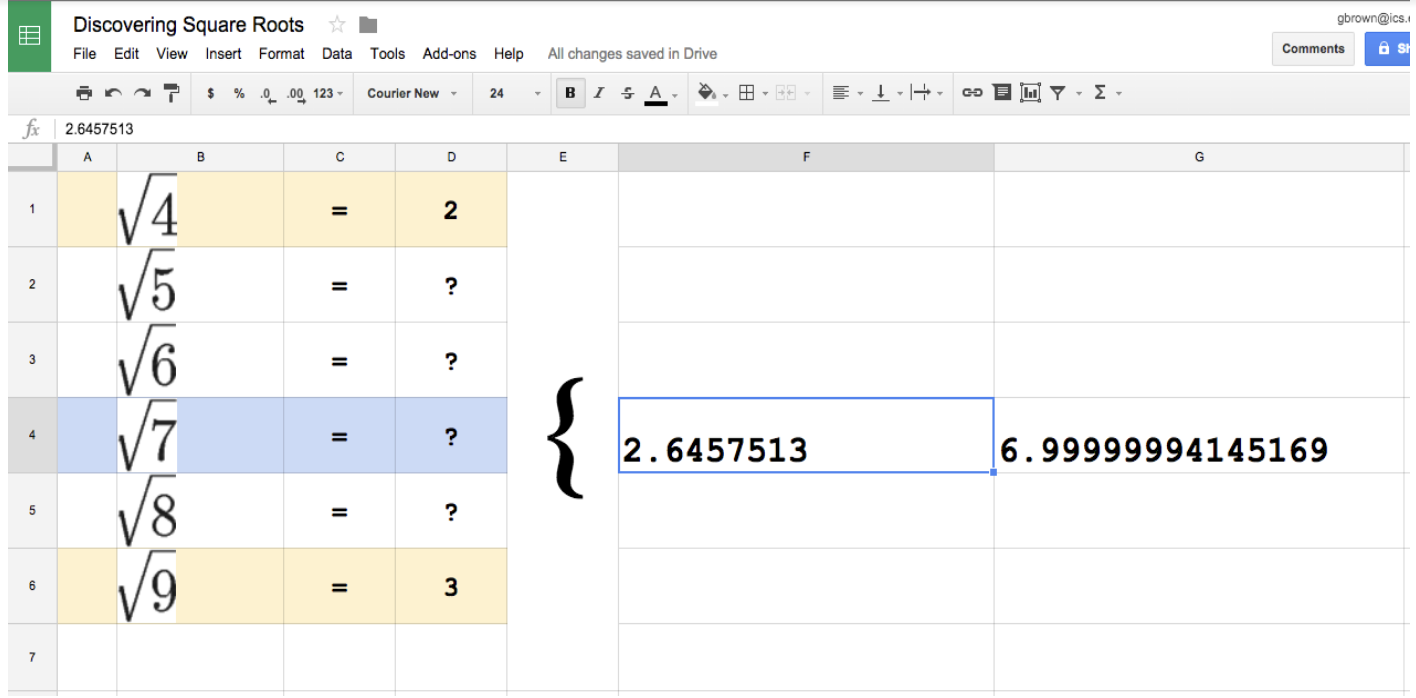
We continue trying to "zoom in" on the answer. As we keep getting closer, we see squares such as 6.99999993 and 7.0000000014. Never, however, do we see exactly 7.0. Each time I've done this activity, I hear an emphatic, "But this is going to go on forever!" This is the hook. This leads to an engaging discussion about irrational numbers, forever, and infinity.
An ancillary benefit from this approach was unexpected but marvelous. Students engaged in guessing in an environment that was safe and fun. This activity established that we can toss around ideas and guesses without the fear of what's right and wrong. I usually plan to have students discover 4-5 decimal places but every time, they ask to continue. Each student wants to try guessing the next number. It's like a game. We find that it's the process and the journey that provides opportunity into learning, not merely the end result.
Here is a link to the spreadsheet. Feel free to copy and make it your own.