I love the practice of revisiting ideas at various levels throughout a curriculum. One excellent candidate is the well known "Box Problem" in which students are asked to construct a box such that the volume is maximized. This problem can be approached in early grades, Algebra, and Calculus. At each level, the problem invites exploration and almost begs for the next level so it can be better understood.

The Box Problem in Early Grades (1-4)
Students may be given a piece of construction paper, a ruler, and some tape. This paper can have a grid already printed and the students must cut out squares for the 4 corners of various sizes. They must cut along the lines provided by the grid. Students could be placed into groups, with each group instructed to create a rectangular box by cutting out corners of different dimensions (some 1x1, some 3x3, etc.). I would purposely leave gaps in the data. Once each group builds their rectangle and computes the volume of their box, the results could be placed into a data table.
Just looking at that table of data, we see many opportunities for various investigations and explorations. Ultimately, the goal is to fill in the remaining rows of the table via induction and determine the maximum volume. Once we do so, we could "build" the boxes we predicted and check our answers. On the way toward that goal, we could ask the students:
It is important to realize the actual goal here is far more than just determining the maximum volume. We are laying the foundation here for Algebra (BoxWidth = PaperWidth - 2H), discrete vs continuous functions (graphing integer solutions and talking about points "in between"), domain/range (H<7), and the inductive method (find rule/equation and calculate other results). Have fun!
The Box Problem in Calculus
The box problem is very well known in Calculus I when discussing Max/Min problems. It's a fun set of problems when taught as traditionally presented. However, here I wish to point out some interesting things I discovered when I presented this problem to a calculus class using a discovery based approach.
First, we used construction paper. I didn't plan it, but it was serendipitous that the dimensions of this paper caused the answer to be irrational. This one coincidence is what made the investigation so rich. No matter what method we used (trial and error, spreadsheet, graphing calculator) we were unable to determine the exact solution. Only the derivative would provide that.
Students built rectangles and we collected our data into a chart. Then, we entered this data into a spreadsheet that I made beforehand. Using integers, we were able to determine that our maximum volume occurs at x=2 (where x equals the length of the sides of the square in each corner to cut out). I created my spreadsheet with a variable called "step" which autofills the square side column. This value was initially set to "1" to show only integer solutions:
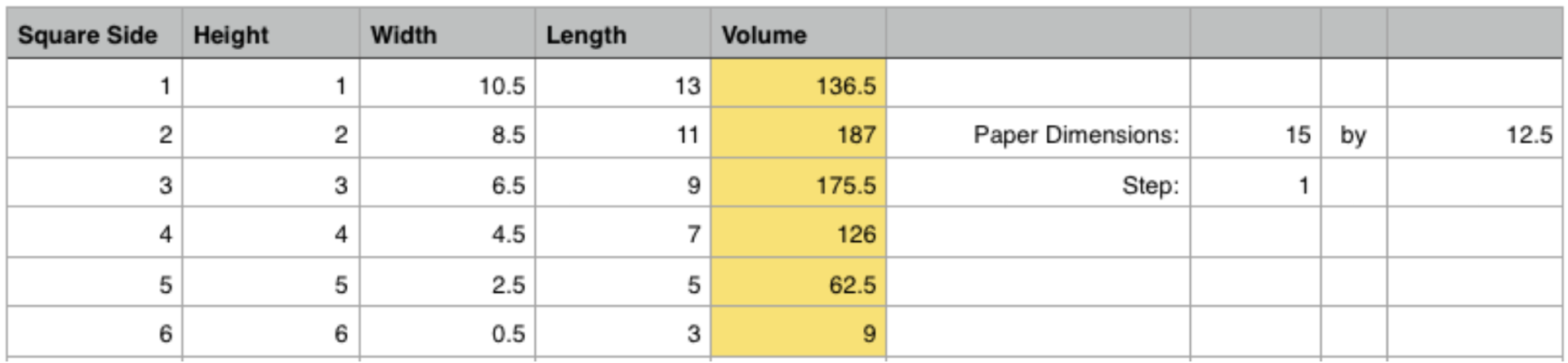
It appears clear that our maximum volume occurs at Height=2. However, if we change the Step from 1 to 0.5, we see a more granular solution:
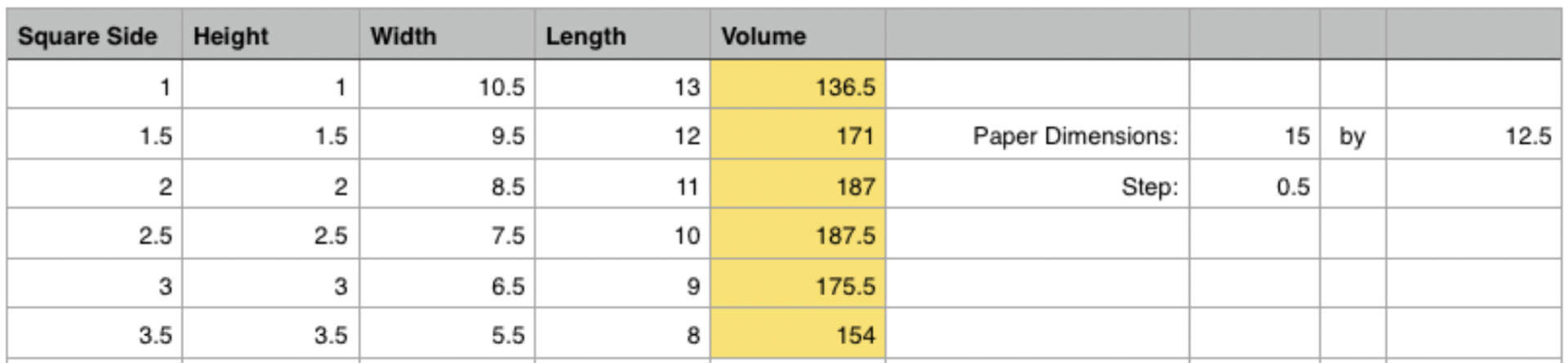
Now, we see that 2.5 actually provides a greater volume than 2.0. At this point, however, most students immediately wonder if there might be an even greater volume between 2 and 2.5 or between 2.5 and 3. Hence, we change our step again (and again and again and again) - continually "zooming in" on the exact solution. In the figure below, we see that for Step=0.001 the maximum volume occurs when Height=2.263. But this number, of course, is 2.2630. What if the maximum is at 2.2632? or 2.2635?
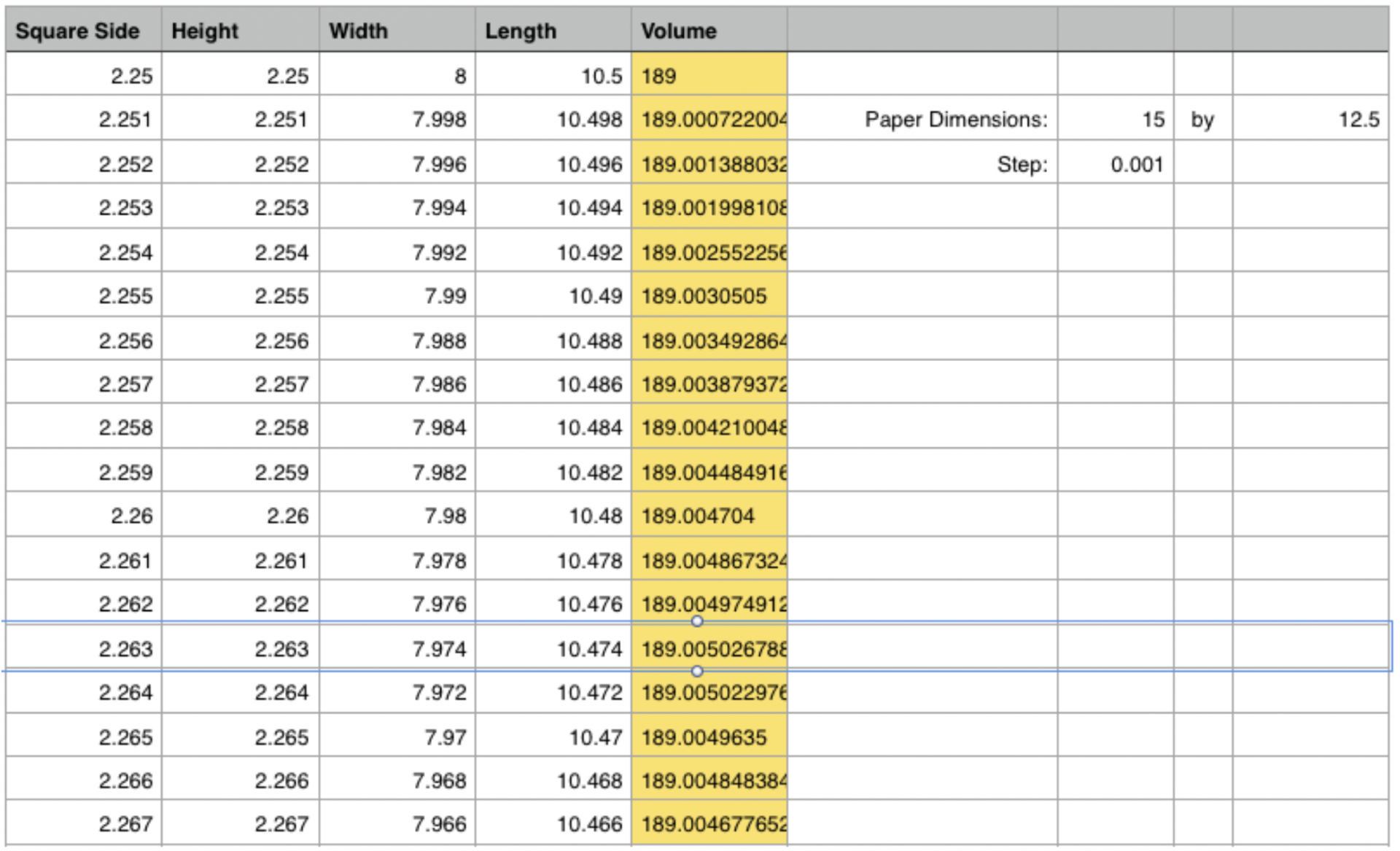
The first time I approached this lesson with a class, the infinite nature of this exploration was unexpected. Ironically, this unexpected aspect is what I think is the most powerful part of this lab. By using the spreadsheet as a tool, we are able to "see" the infinite nature of the limit in calculus. We are also able to see the futility of crunching numbers ad infinitum. Hence, we realize the beauty and power of the limit (or calculus).
Contrast the traditional approach
By contrast, let's look at the approach using the derivative:
1. Write the equation for the Volume: V = (15 - 2x)(12.5 - 2x)(x)
2. Multiply to arrive at: V = 4x^3 - 55x^2 + 187.5x
3. Take the derivative: V' = 12x^2 - 110x + 187.5
4. Set the derivative equal to zero and solve with the quadratic formula: x = 6.90... and 2.26...
5. The 6.9 solution exceeds the domain. Thus, the max volume occurs at x = 2.2634315154874907...
Note how simple the problem is and how, as a result of the computational simplicity, the underlying concepts remain hidden. These concepts are what the inductive approach allows students to see.
QED.
